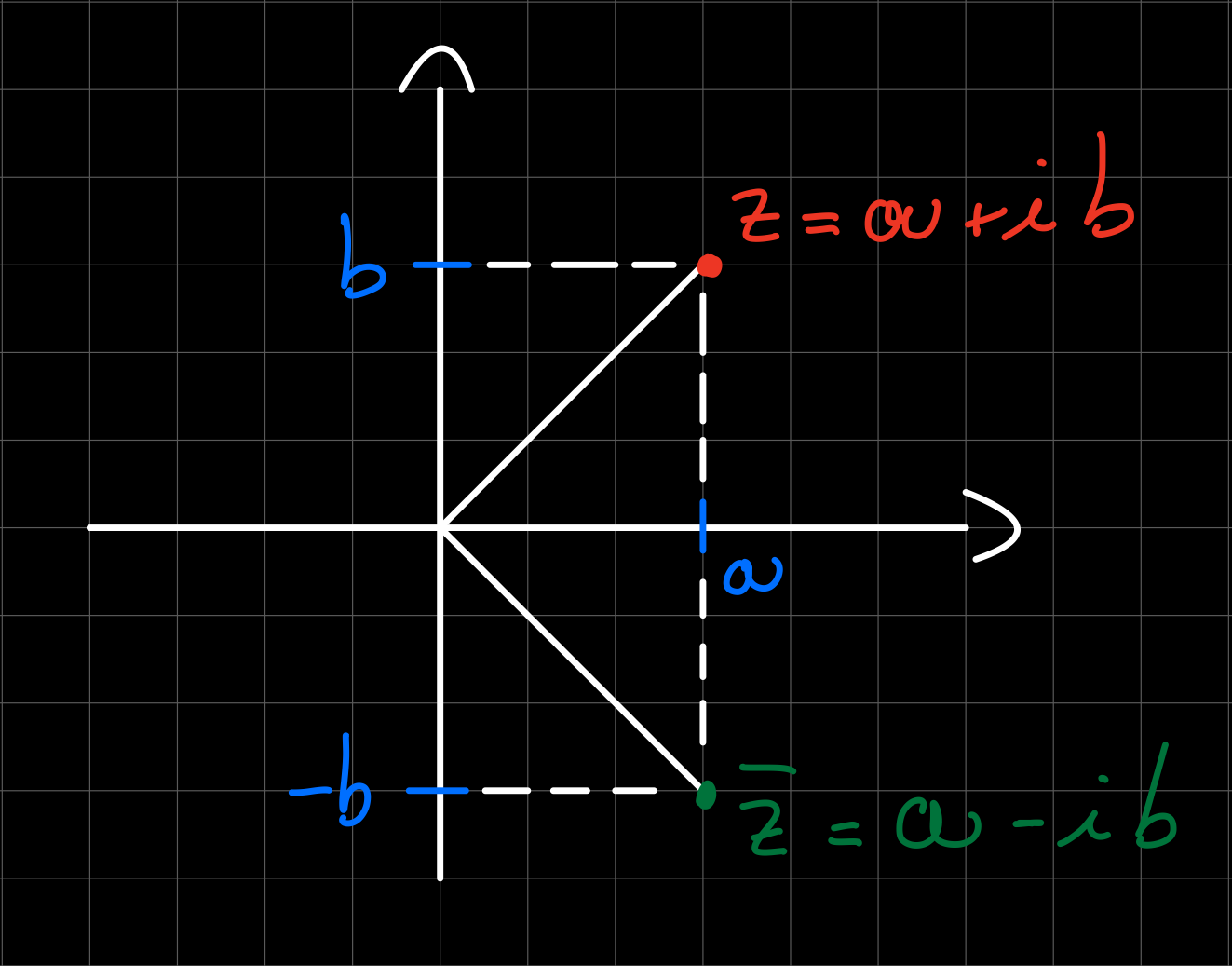Skip to main content

Coniugato e modulo

Sia z=a+ibz = a + ib.

Si definisce coniugato di zz:

z‾=a−ib\overline{z} = a - ib.

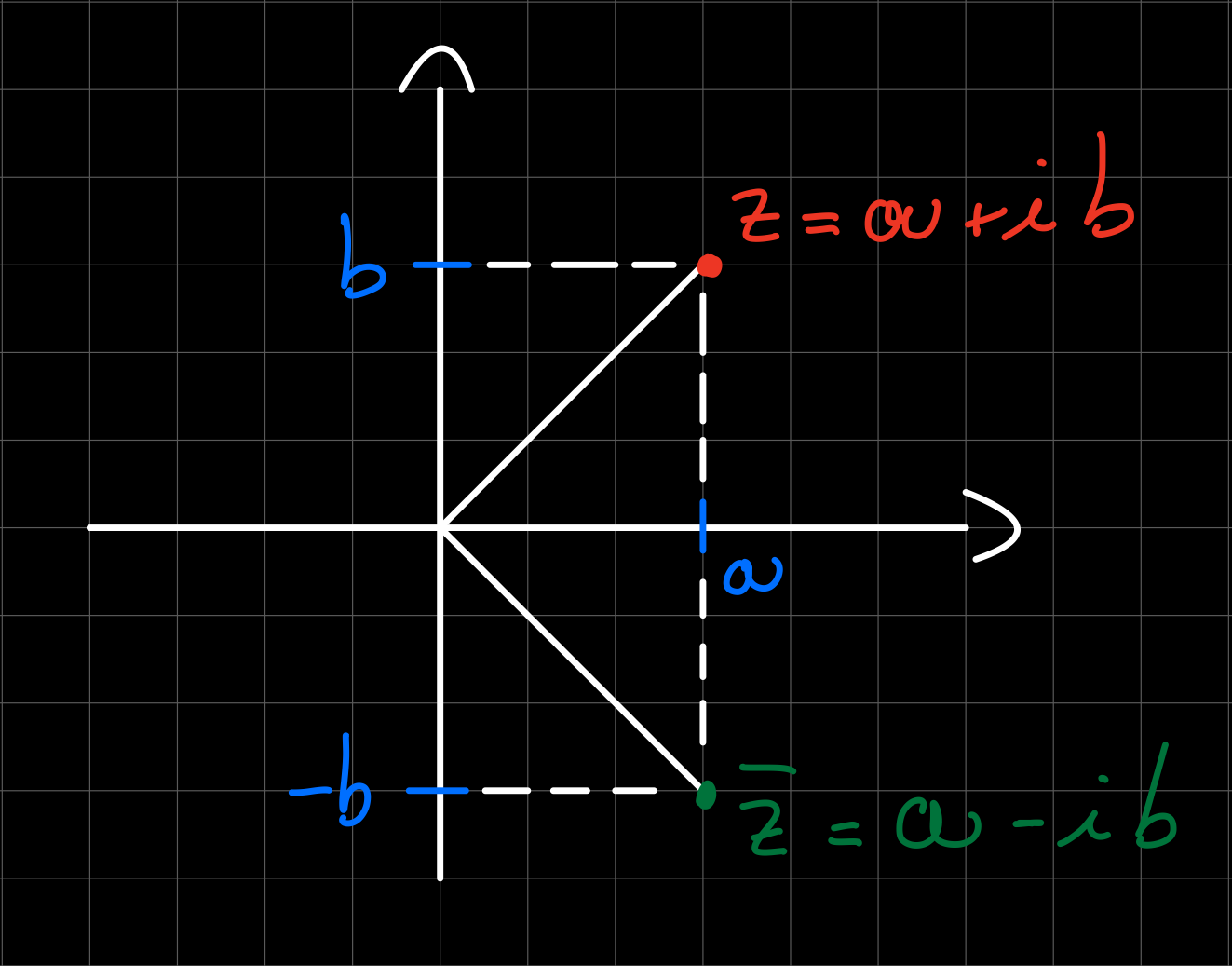
Grafico numero coniugato

Proprietà del numero coniugato​

  1. z+z′‾=z‾+z′‾\overline{z + z'} = \overline{z} + \overline{z'}

  2. z∗z′‾=z‾∗z′‾\overline{z * z'} = \overline{z} * \overline{z'}

  3. Se z≠0:1z‾=1zz \neq 0: \overline{\frac{1}{z}} = \frac{1}{z}

  4. z∗z′=(a+ib)∗(a−ib)=a2−i2b2=a2+b2=∣z∣2z * z' = (a + ib) * (a - ib) = a^2 - i^2b^2 = a^2 + b^2 = |z|^2

  5. Se z≠0:z∗1z′‾=zz′‾=z‾z′‾z \neq 0: \overline{z * \frac{1}{z'}} = \overline{\frac{z}{z'}} = \frac{\overline{z}}{\overline{z'}}

    Infatti z‾z′=z∗1z′‾\frac{\overline{z}}{z'} = \overline{z * \frac{1}{z'}}.

    Applichiamo la proprietà 2 z‾∗1‾z′‾\overline{z} * \frac{\overline{1}}{\overline{z'}}.

    Applichiamo la proprietà 3 z‾∗1z′‾=z‾z′‾\overline{z} * \frac{1}{\overline{z'}} = \frac{\overline{z}}{\overline{z'}}.

  6. Se z≠0:1z=z‾∣z∣2z \neq 0: \frac{1}{z} = \frac{\overline{z}}{|z|^2}

    Infatti z∗z‾∣z∣2=z∗z′‾∣z∣2z * \frac{\overline{z}}{|z|^2} = \frac{z * \overline{z'}}{|z|^2}.

    Applichiamo la proprietà 4 ∣z∣2∣z∣2=1\frac{|z|^2}{|z|^2} = 1

Modulo di un numero complesso​

Si definisce modulo di z ∣z∣=a2+b2|z| = \sqrt{a^2 + b^2}.

Esempio​

Partiamo dal numero z=1+i2−iz = \frac{1 + i}{2 - i}

Troviamo il suo coniugato​

Applichiamo la proprietà 5

z‾=1+i‾2−1‾=1−i2+i\overline{z} = \frac{\overline{1 + i}}{\overline{2 - 1}} = \frac{1 - i}{2 + i}

Troviamo il suo modulo​

Applichiamo la proprietà 4

∣z∣=z∗z′‾=1+i2−1∗1−i2+i|z| = \sqrt{z * \overline{z'}} = \sqrt{\frac{1 + i}{2 - 1} * \frac{1 - i}{2 + i}}

Troviamo la forma algebrica di z​