Statistica descrittiva

Cos'è la statistica ?

Esistono due tipi di statistiche:

• Statistica descrittiva, parte della statistica che si occupa di raccogliere i dati e di sintetizzarne alcune informazioni
• Statistica inferenziale, parte della statistica che crea le conclusioni una volta ottenuti i dati da osservare.

Qual è lo scopo generale della statistica ?

Lo scopo generico della statistica è quello di studiare una popolazione di elementi per trarne delle conclusioni.

Cosa sono la popolazione e i campioni ?

La popolazione è collezione totale di elementi su cui vogliamo concentrare la analisi statistica.

La statistica descrittiva ha poi il compito di estrarre dalla popolazione, il cosiddetto campione, ovvero un insieme di sotto-elementi della popolazione che viene scelto in base ai parametri della nostra analisi.

Tabella delle frequenze e grafici

• La funzione stem() permette di visualizzare una tabella delle frequenze su un grafico formato a linee verticali (Line Graph)
• La funzione plot() permette di visualizzare una tabella delle frequenze su un grafico formato da una linea continua che connette i diversi valori della variabile (Frequency Poligon)
• La funzione bar() permette di visualizzare una tabella delle frequenze su un grafico a barre (Bar Graph)
• La funzione pie() permette di visualizzare un grafico a torta (Pie Chart)
• La funzione pie3() permette di visualizzare un grafico a torta in versione 3D (3D Pie Chart)
• La funzione histogram() permette di visualizzare un istogramma (Histogram)

Frequenza relativa

La frequenza relativa non è altro che il rapporto tra il valore della variabile / il numero totale di elementi presi in considerazione.

Grafico a torta

Moltiplicando la frequenza relativa di un settore per 360 gradi, è possibile scoprire i gradi del settore.

Es: supponiamo che la frequenza relativa sia 0.333%, per trovare l'angolo è sufficiente fare 360 * 0.333 ottenendo 119.88 gradi.

Come fare per suddividere l'insieme di dati ?

Quando è presente un numero di elementi distinti troppo grande per essere utilizzato direttamente, è possibile suddividere gli elementi in gruppi detti classi.

C'è da porre attenzione nella scelta, perchè:

• In caso le classi siano troppo poche, c'è il rischio di perdita di informazione.
• In caso le classi siano troppe, c'è il rischio che le frequenze di ogni classe siano troppo piccole per poter essere analizzate correttamente.

Che cos'è un istogramma (Histogram) ?

E' un grafico con barre adiacenti, dove le barre rappresentano le classi di dati disponibili.

Consente di capire la forma della distribuzione dei valori d'analisi.

Solitamente, nell'asse y dell'istogramma vi è la frequenza relativa, e le classi nell'asse x, ma non è obbligatorio ne vincolante.

Le caratteristiche individuabili dal grafico sono:

• La simmetria del grafico
• Il grado di diffusione dei dati, e capire sono adiacenti, sparsi o concentrati in poche classi
• Capire se vi sono "buchi" tra tipologie di classi

Quali errori possono verificarsi negli istogrammi ?

• La suddivisione in troppe classi può creare una forma scomposta
• Scegliere tante classi, ed inserire pochi valori di riferimento nell'asse x, crea un grafico poco leggibile, perchè tra l'intervallo di valori scelti sono presenti molte classi
• Le label del grafico devono contenere le unità di misura

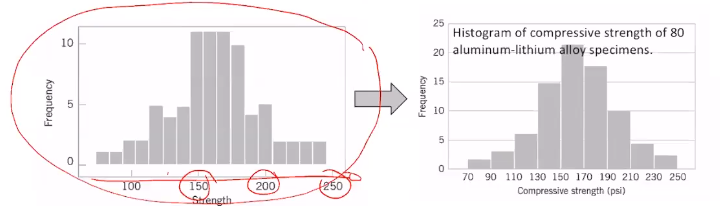
Grafico delle frequenze cumulative (ogive)

Questa tipologia di grafico viene sempre messa in combinazione con un istogramma.

Dato un determinato valore che vogliamo utilizzare, possiamo capire qual è il numero della frequenza che sta al di sotto del valore.

Come si può riassumere il nostro dataset?

E' possibile riassumere un dataset fornendo le seguenti informazioni:

• Una misura di locazione o centralità dei dati (es: mediana e/o media campionaria)
• Una misura di dispersione dei dati, ovvero quanta variazione vi è rispetto ad una misura di locazione come la media (es: deviazione e/o un range interquantile)
• Una misura di forma dei dati, ovvero la distribuzione dei dati (es: skewness e una misura di kurtosis)

Concetto di media campionaria

La definizione matematica di media campionaria è:

$\overline{x}$ = $\sum_{i=1}^{(n)} \frac{x_i}{n}$

Supponendo di avere quindi in insieme di dati formato da $y_1, ... y_n$ otteniamo:

$y_i = ax_i + b$

$i = 1, ... n$

$\overline{y} = \sum_{i=1}^{(n)} \frac{(ax_i + b)}{n} = \sum_{i=1}^{(n)} \frac{ax_i}{n} + \sum_{i=1}^{(n)} \frac{b}{n} = a\overline{x} + b$

---

Forniamo ora un esempio concreto:

Abbiamo come dataset una serie di punteggi vincenti di golf dal 1982 al 1991, e vogliamo trovarne la media:

284, 280, 277, 282, 279, 285, 281, 283, 278, 277

Soluzione

Scegliamo un numero arbitrario per ottenere dei valori più piccoli su cui lavorare, in questo caso il 280.

Andiamo quindi a sottrarre 280 a tutti i numeri, e creare così un nuovo dataset con numeri più piccoli.

Otteniamo quindi un nuovo dataset formato da:

4, 0, -3, 2, -1, 5, 1, 3, -2, -3

Collegandoci quindi alla formula, il nostro 280 assume il valore della costante B, trasformando l'equazione in:

$y_i = ax_i - 280$ .

Eseguiamo quindi ora la media del nuovo dataset.

Alla fine del risultato, va poi riaggiunto il valore iniziale tolto, in questo caso 280.

$\overline{y} = \frac{6}{10}$ -> $\overline{x} = \overline{y} + 280 = 280.6$

Come fare la media campione ad una tabella di frequenze ?

E' necessario creare una lista dei valori distinti associati alle frequenze.

Supponendo che i valori siano K, avremo quindi $v_1, ... v_k$ valori corrispondenti a $f_1, ... f_k$ frequenze.

Una volta creato l'insieme dei valori distinti, è sufficiente sommare le frequenze tra di loro per trovare la nostra variabile N, quindi:

$n = \sum_{i=1}^{k} f_i$

Infine, la media dei valori distinti si ottiene con:

$\overline{x} = \sum_{i=1}^{k} \frac{v_i*f_i}{n}$

Come calcolare la mediana

Per effettuare la mediana è necessario:

• Ordinare tutti gli elementi dal più piccolo al più grande
• Se il numero totale degli elementi è dispari, la mediana si calcola con $\frac{n+1}{2}$
• Se il numero totale degli elementi è pari, la mediana corrisponde alla divisione tra i valori in posizione $\frac{n}{2}$ e $\frac{n}{2} + 1$

Che differenza c'è tra la mediana e la media campione ?

La media campione utilizza tutti gli elementi dell'insieme di dati scelto, tendendo a spostarsi di molto quando la distribuzione degli elementi è poco bilanciata (magari con estremi molto grandi).

La mediana utilizza invece i campioni centrali della distribuzione, non risentendone dei valori estremi del dataset.