Vettori

Coordinate polari

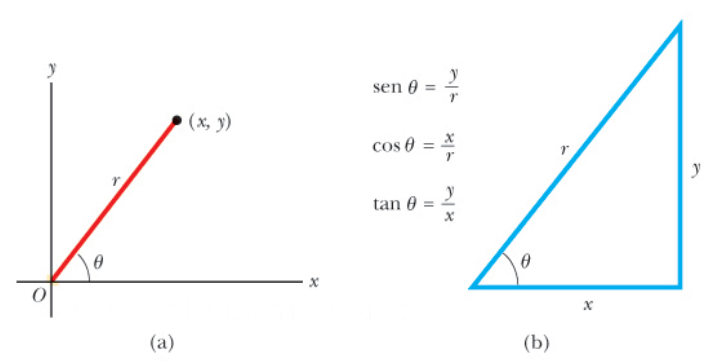
1. $r$ rappresenta la distanza dal punto $P$ dall'origine

2. L'angolo tra l'asse delle ascisse (x) ed il segmento $r$ viene chiamato theta $\theta$.

3. Andiamo quindi a formare un triangolo rettangolo, con i valori calcolabili tramite le seguenti formule:

   $x = r*\cos{\theta}$

   $y = r*\sin{\theta}$

   $tan \theta = \frac{y}{x}$

   $r = \sqrt{x^2+y^2}$ - Teorema di pitagora

Che cos'è un vettore ?

Una grandezza è vettoriale quando per essere definita ha bisogno di:

• Un valore con relativa unità di misura (detto modulo del vettore)
• Una direzione
• Un verso

Rappresentazione algebrica di un vettore: $\vec{A}$

Rappresentazione del modulo di un vettore: $|\vec{A}|$

Uguaglianza tra due vettori

Due vettori $\vec{A}$ e $\vec{B}$ sono uguali se e solo se:

• Hanno modulo uguale
• Hanno direzione uguale
• Hanno verso uguale

Nota bene: l'uguaglianza tra due vettori è indipendente dal punto di origine dei due vettori in confronto.

Operazioni con i vettori tramite metodo grafico

Somma tra vettori

La somma tra un vettore $\vec{A}$ ed un vettore $\vec{B}$ corrisponde ad un nuovo vettore (detto risultante) $\vec{R}$ e definito come:

$\vec{R} = \vec{A} + \vec{B}$

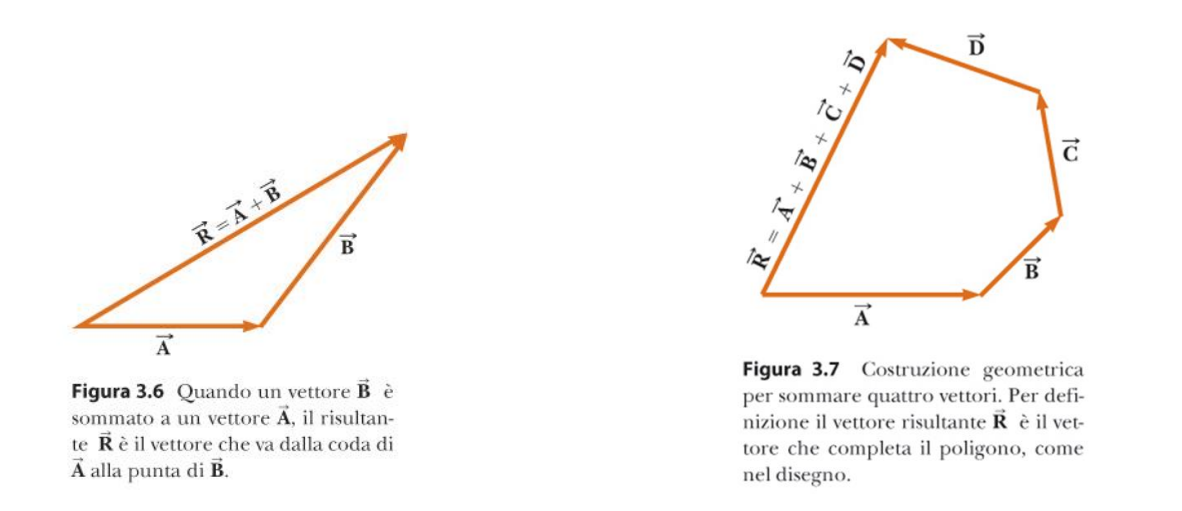
Proprietà della somma tra vettori

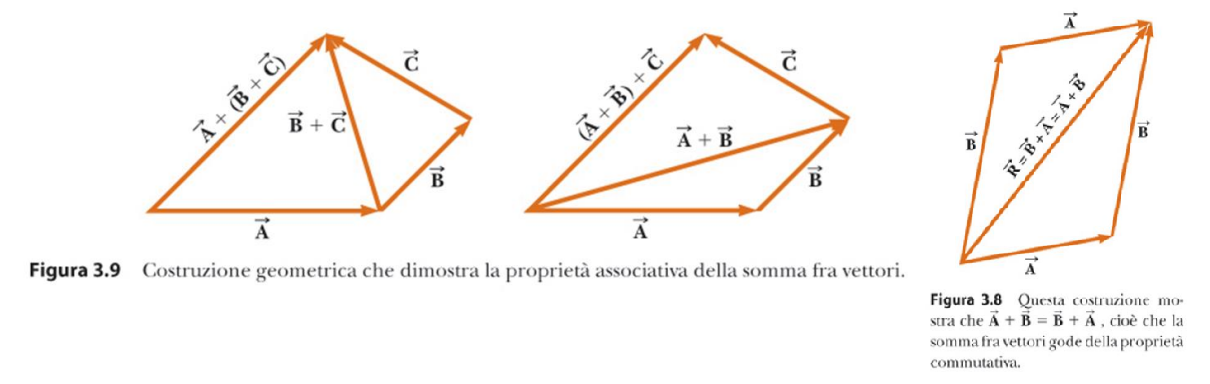
• Proprietà cumulativa: $\vec{A} + \vec{B} = \vec{B} + \vec{A}$
• Proprietà associativa: $\vec{A} + (\vec{B} + \vec{C}) = \vec{B} + (\vec{A} + \vec{C})$
• Proprietà del vettore opposto: un vettore che se sommato al vettore $\vec{A}$ ci da $0$, quindi il vettore $-\vec{A}$.

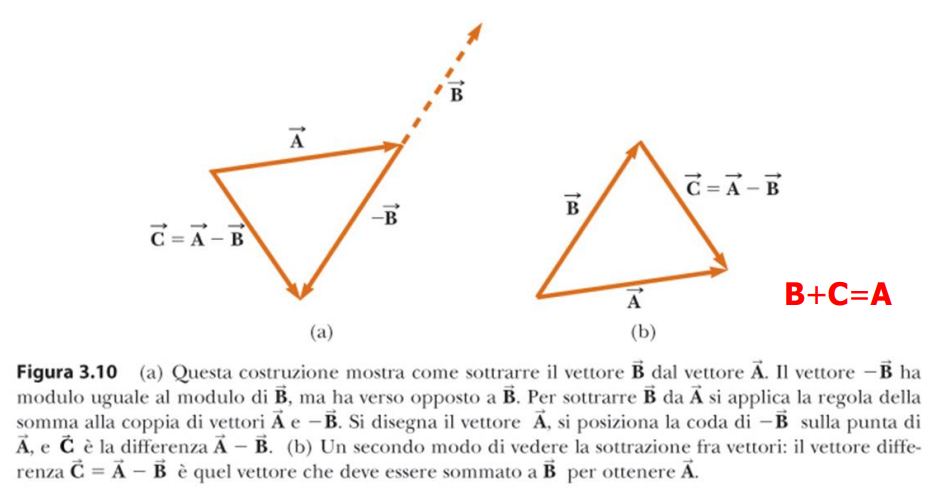
Sottrazione tra vettori

La sottrazione $\vec{A} - \vec{B}$ si esegue considerando $- \vec{B}$ come l'opposto del vettore $\vec{B}$.

Si può quindi scrivere l'operazione come: $\vec{A} - \vec{B} = \vec{A} - (+ \vec{B})$.

Moltiplicazione tra un vettore ed un numero scalare

• Se il numero scalare $m$ è positivo, il vettore risultante della moltiplicazione $m\vec{A}$, ha come modulo $|mA|$ e come direzione e verso quelle del vettore $\vec{A}$.
• Se il numero scalare $m$ è negativo, il vettore risultante della moltiplicazione $-m\vec{A}$, ha come modulo $|mA|$, come direzione quella di A, e verso opposto a quello di A.

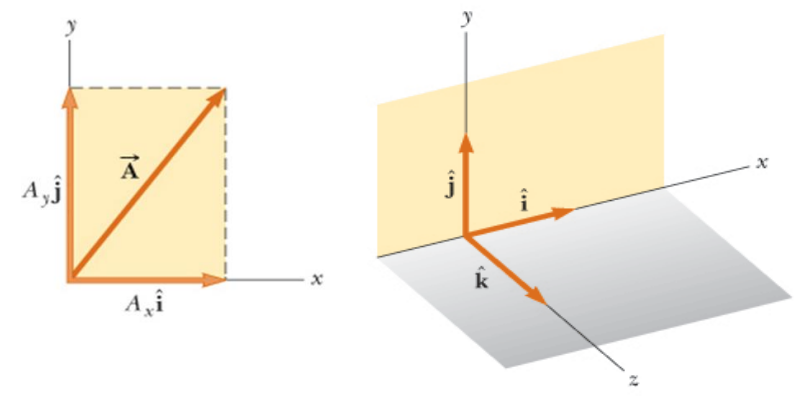
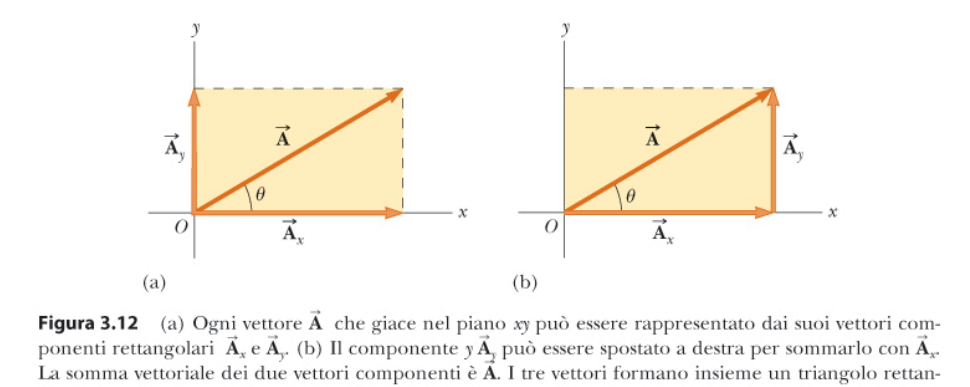
Componenti di un vettore

Supponiamo di avere un vettore $\vec{A}$.

Inserendo il vettore $\vec{A}$ sul piano cartesiano, è possibile vedere due distinti componenti che formano il vettore $\vec{A}$:

• Il vettore $\vec{A_x}$ che rispecchia il vettore $\vec{A}$ sull'asse $x$
• Il vettore $\vec{A_y}$ che rispecchia il vettore $\vec{A}$ sull'asse $y$

La somma di questi due vettori componenti, fa quindi il vettore $\vec{A}$.

Le formule esatte sono:

$A_x = A * \cos{\theta}$

$A_y = A * \sin{\theta}$

$A = \sqrt{A^2_x + A^2_y}$

$\theta = \frac{1}{\tan{\frac{A_y}{A_x}}} => \theta = \tan^{-1}{\frac{A_y}{A_x}}$

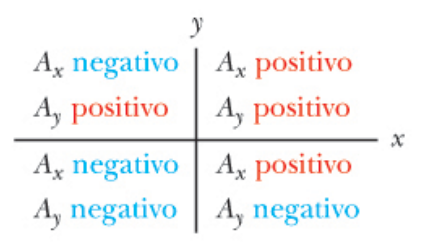
Segni dei componenti nel piano cartesiano

Vettore unitario (o versore)

Un vettore unitario è un vettore adimensionale il cui modulo è 1.

Un vettore unitario si utilizza per individuare una direzione ed un verso nello spazio.

Supponendo che:

• $\hat{i}$ sia sull'asse x
• $\hat{j}$ sia sull'asse y
• $\hat{i}$ sia sull'asse z

è possibile dire che i vettori $\hat{i}$, $\hat{j}$ e $\hat{k}$ individuano nello spazio il verso e la direzione dei rispettivi assi.

I loro moduli sono uguali e costanti a 1, $|\hat{i}| = |\hat{j}| = |\hat{k}| = 1$.

$\vec{A_x} = A_x * \hat{i}$

$\vec{A_y} = A_y * \hat{j}$

$\vec{A} = (A_x * \hat{i}) + (A_y * \hat{j})$